Khối đa diện đều thường là khái niệm thường được sử dụng trong hình học và nhiều người băn khoăn về có bao nhiêu loại khối đa diện đều. Cùng Trung tâm sửa chữa điện lạnh – điện tử Limosa tìm hiểu ngay dưới đây nhé!

1. Khối đa diện đều là gì?
Câu hỏi về có bao nhiêu loại khối đa diện đều thì khái niệm về khối đa diện đều là một dạng khối đa diện lồi (là khối đa diện mà trong với bất kì hai điểm A, B nào cũng đều có thể thuộc nó thì ở trong mọi điểm của đoạn AB cũng thuộc nó) có thể có thêm hai tính chất sau đây:
- Mỗi mặt là một đa giác đều n cạnh (n-giác đều)
- Mỗi đỉnh là đỉnh chung của đúng p mặt.
2. Có bao nhiêu loại khối đa diện đều?
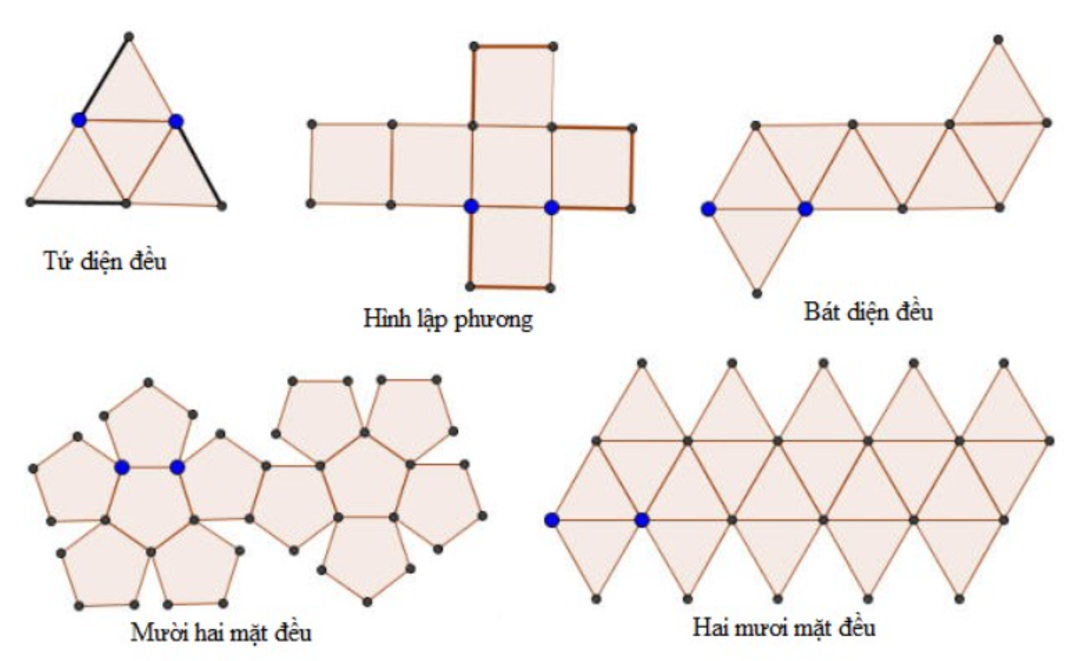
Câu hỏi khối đa diện đều có bao nhiêu loại thì người ta chứng minh được chỉ có 5 loại khối đa diện đều. Đó là các loại: {3;3}, {4;3}, {3;4}, {5;3} và {3;5}. Tên gọi tương ứng được cho trong bảng dưới đây.
- Số cạnh số đỉnh dựa trên số mặt của năm loại khối đa diện đều
- Khối đa diện đều loại {n,p} có Đ đỉnh, C cạnh và M mặt thì ta luôn có thêm hằng đẳng thức:
- Đ+M-C=2 và
- pĐ=2C=nM
- Khối đa diện đều như vậy gọi là khối đa diện đều loại {n, p}.
Có bao nhiêu loại khối đa diện đều thì 5 khối đa diện đều, đó là sẽ là tứ diện đều, hình lập phương, hình bát diện đều, hình mười hai mặt đều, hình hai mươi mặt đều.
Có 5 khối đa diện đều, đó là tứ diện đều (loại {3; 3}), hình lập phương (loại {4; 3}), hình bát diện đều (loại {3; 4}), hình mười hai mặt đều (loại {5; 3}), hình hai mươi mặt đều (loại {3; 5}), các mặt của khối đa diện đều là những đa giác đều bằng nhau.
Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
- Mỗi mặt của nó là một đa giác đều p cạnh.
- Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Trong khối đa diện đều có bao nhiêu loại thường sẽ như vậy được gọi là khối đa diện đều loại {p ; q}.
Các mặt của khối đa diện đều là những đa giác đều bằng nhau.
Chỉ có năm khối đa diện đều. Đó là:
- Loại {3; 3}: khối tứ diện đều.
- Loại {4; 3}: khối lập phương.
- Loại {3; 4}: khối bát diện đều.
- Loại {5; 3}: khối 12 mặt đều.
- Loại {3; 5}: khối 20 mặt đều.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo theo thứ tự được gọi là khối đa diện đều, khối lập phương, khối tám mặt đều, khối mười hai mặt đều, khối hai mươi mặt đều.
Một khối đa diện lồi là đều nếu và chỉ nếu thỏa mãn cả ba tính chất sau
- Tất cả các mặt của nó là các đa giác đều, bằng nhau
- Các mặt không cắt nhau ngoài các cạnh
- Mỗi đỉnh là giao của một số mặt như nhau (cũng là giao của số cạnh như nhau).
- Mỗi khối đa diện đều có thể xác định bới ký hiệu {p, q} trong đó
- p = số các cạnh của mỗi mặt (hoặc số các đỉnh của mỗi mặt)
- q = số các mặt gặp nhau ở một đỉnh (hoặc số các cạnh gặp nhau ở mỗi đỉnh).
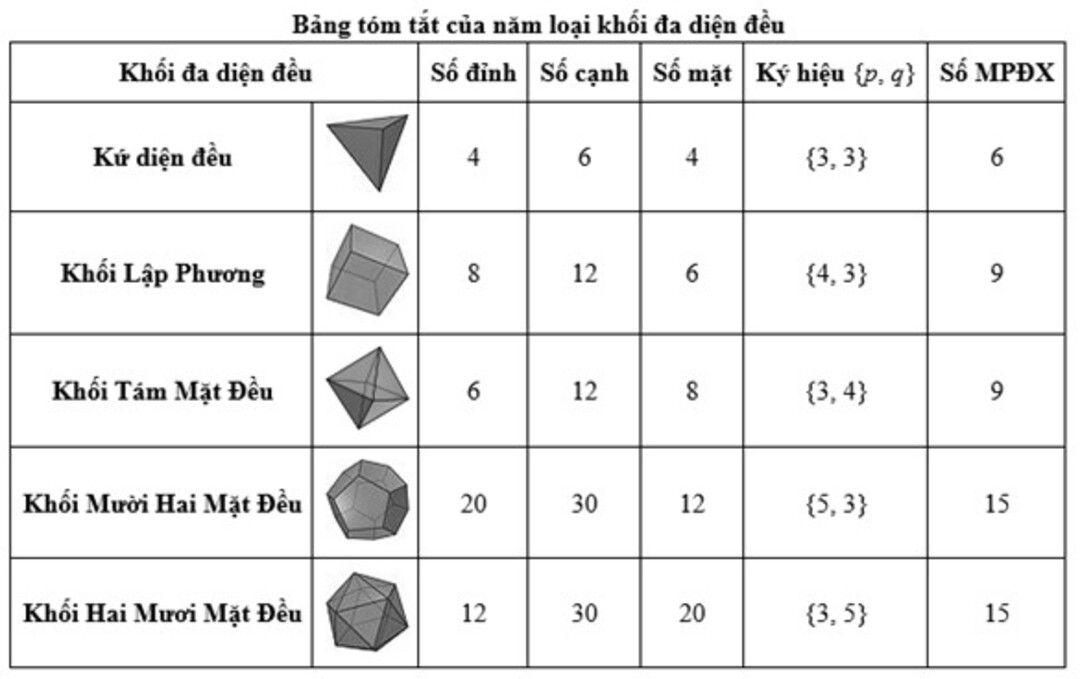
- Khí hiệu {p, q}, được gọi là ký hiệu Schläfli, là đặc trưng về số lượng của khối đa diện đều. Ký hiệu Schläfli của năm khối đa diện đều được cho trong bảng sau.
- Khối đa diện đều loại {n;p} có Đ đỉnh, C cạnh và M mặt thì: pĐ=2C=nM
- Định lý Ơ-le: Mọi khối đa diện lồi đều có D−C+M=2, ở đó D,C,M lần lượt là số đỉnh, số cạnh, số mặt của khối đa diện.
3. Đặc điểm, tính chất về khối đa diện
Một số đặc điểm và tính chất về có bao nhiêu loại khối đa diện đều mà học sinh cần nhớ khi tiến hành làm các bài tập khối đa diện như sau:
Tính chất 1: Cho một khối tứ diện đều, ta có:
- Đỉnh của một khối tứ diện đều khác là trọng tâm của các mặt.
- Trung điểm của mọi cạnh chính là các đỉnh của khối bát diện đều.
Tính chất 2: Cho khối lập phương, tâm các mặt của nó sẽ tạo thành 1 khối bát diện đều.
Tính chất 3: Cho khối bát diện đều, tâm các mặt của nó sẽ tạo thành một khối lập phương.
Tính chất 4: Hai đỉnh của một khối bát diện đều được gọi là hai đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối bát diện đều. Khi đó:
- Ba đường chéo giao nhau tại vị trí trung điểm của mỗi đường.
- Ba đường chéo vuông góc với nhau theo từng đôi một.
- Ba đường chéo bằng nhau.
Tính chất 5: Một khối đa diện phải có tối thiểu 4 mặt.
Tính chất 6: Hình đa diện có tối thiểu 6 cạnh.
Tính chất 7: Không tồn tại đa diện có 7 cạnh.
Những thông tin về có bao nhiêu loại khối đa diện đều hy vọng đã giúp bạn có thể hiểu rõ được những khối đa diện đều trong toán học. Nếu còn bất kỳ thắc mắc nào cần lời giải đáp hãy liên hệ ngay HOTLINE 1900 2276 của Trung tâm sửa chữa điện lạnh – điện tử Limosa nhé!
